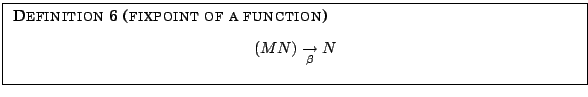



Next: Generation of fixpoint using
Up: Basic Usage of Y-Combinator
Previous: Basic Usage of Y-Combinator
Contents
Start
If it can be shown that
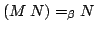 is true, then
is true, then 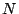 is
called either a `fixed point' or a `fixpoint' of
is
called either a `fixed point' or a `fixpoint' of 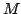 .
.
According to H. Curry, there exists a function, that
generates such a fixed point of 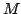 . This function is
the so-called Y-combinator introduced above.
. This function is
the so-called Y-combinator introduced above.
According to the above definition a fixpoint of a function can be
seen as a lambda expression that, if passed as argument to this
function is returned by the function.
Georg P. Loczewski
2004-03-05
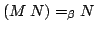 is true, then
is true, then ![]() . This function is
the so-called Y-combinator introduced above.
. This function is
the so-called Y-combinator introduced above.